Quelques éléments sur le binaire, l'hexadécimal, le microprocesseur

Cette page est loin d'être un cours de programmation. Elle rassemble simplement quelques éléments importants.

L'informatique utilise le code binaire pour toutes ses opérations.
L'explication vient du fait que les premiers ordinateurs fonctionnaient à l'aide de composants (lampes, puis transistors, puis circuits intégrés, puis microprocesseurs) qui avaient deux états, comme un interrupteur :

• ouvert = coupé, représenté par un 0
• fermé = passant, représenté par un 1

Les composants électroniques mentionnés ci-dessus permettent de réaliser des fonctions 'logiques' de base.

La transposition mathématique s'appelle 'Algèbre de Boole' et les fonctions précédentes deviennent des 'opérateurs booléens'.

On appelle table de vérité, un tableau qui indique le résultat d'une opération données pour toutes les valeurs possibles des variables d'entrée..

Voici les 4 fonctions électroniques et les opérateurs associés :

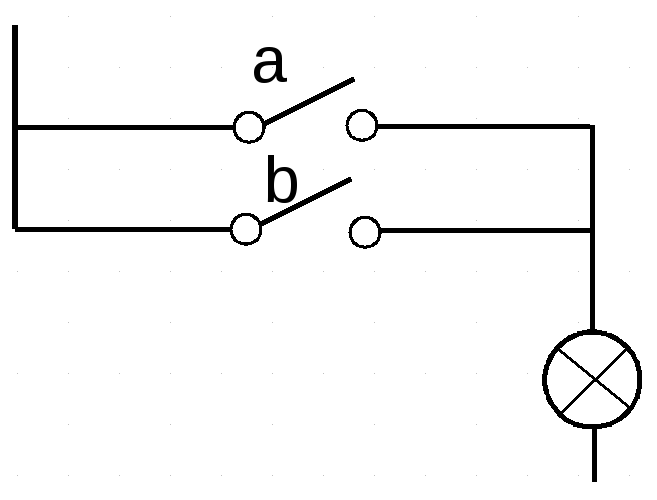• OU : dans le schéma ci-contre, il suffit que l'un ou l'autre des interrupteurs soit fermé (survolez l'image avec la souris pour agrandir).
  La table de vérité est la suivante :
  

  Entrée1 : a	Entrée2 : b	Sortie : a OU b
  0	0	0
  1	0	1
  0	1	1
  1	1	1

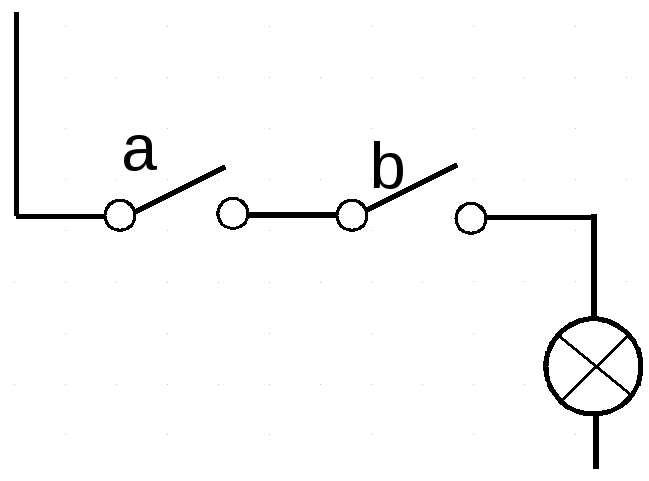• ET : dans le schéma ci-contre, il faut que l'un et l'autre des interrupteurs soient fermés (survolez l'image avec la souris pour agrandir).
  La table de vérité est la suivante :
  

  Entrée1 : a	Entrée2 : b	Sortie : a ET b
  0	0	0
  1	0	0
  0	1	0
  1	1	1

• OU EXCLUSIF : ici aussi, il suffit que l'un ou l'autre des entrées soit à 1, mais pas les deux simultanément.
  La table de vérité est la suivante :
  

  Entrée1 : a	Entrée2 : b	Sortie : a XOU b
  0	0	0
  1	0	1
  0	1	1
  1	1	0

• NON : ici la sortie est simplement l'inverse de l'entrée.
  La table de vérité est la suivante :
  

  Entrée : a	Sortie : NON a
  0	1
  1	0

Comme indiqué plus haut, l'ordinateur ne comprend que le binaire. Il faut donc coder les divers éléments.

Tous les éléments de notre code décimal habituel peuvent être représentés en codage binaire. L'élément de base s'appelle un bit (b).
La figure ci-contre montre la correspondance entre notre système décimal bien connu et son codage en système binaire (survolez l'image avec la souris pour agrandir).

On voit que la valeur de chaque nouveau bit correspond à une puissance de deux : 1, 2, 4, 8, 16 ...

On voit également que, très rapidement, il faudra beaucoup de bits pour coder un nombre, même de faible valeur.
C'est pour cette raison que l'on a introduit deux nouvelles notions :

• l'octet (o) ou byte (B) : c'est un ensemble de 8 bits.
  Si on continuait la table ci-contre, on verrait qu'avec un octet on peut représenter les valeurs 0 à 255
• le codage hexadécimal. Il utilise les symboles du décimal auxquels on ajoute les symboles A, B, C, D, E, F, soit 16 symboles.
  Ceci correspond à une puissance de deux et est ainsi bien approprié pour une représentation du binaire. La figure montre la correspondance entre décimal, binaire et hexadécimal.
  En continuant la table, on verrait que la plus grande valeur que l'on peut écrire avec un octet correspond à 11111111 en binaire et à FF en hexadécimal.

C'est lui qui traite les données en fonction d'un programme qui lui a été donné.
Il lit le programme et exécute les instructions.

Afin de ne pas compliquer inutilement cette initiation, vous ne trouverez que le cas du processeur 16 bits, c'est-à-dire un processeur dont la taille des registres généraux est de 16 bits. Par registres généraux on entend les registres servant dans le jeu d'instructions du processeur. (Voir Introduction à la programmation / Notions de base). Actuellement les registres ont 32 voire 64 bits. Le jeu d'instructions devient de plus en plus important.

La plupart des opérations d'un microprocesseur s'effectuent dans un registre, entre deux registres, entre un registre et la mémoire.
Voici la liste des registres, avec leur taille et leur fonction, pour une architecture appelée x86 16 bits. Elle correspond aux processeurs Intel, jusqu'au 80286. Pour des raisons de compatibilité, les programmes actuels peuvent toujours les utiliser.

En mode réel, l'adresse d’un octet en mémoire est définie sur 20 bits, ce qui correspond à 1 Mo.

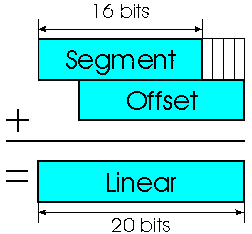
Mais les registres du processeur n'ont que 16 bits. Il faut donc utiliser deux registres pour adresser toute la mémoire : un registre de segment et un registre d'offset.
L'adresse effective est déterminée de la façon suivante : la valeur du segment est multipliée par 16 (ce qui correspond à un décalage de 4 bits vers la gauche) et l'offset est ajouté au résultat.

Une adresse s'écrit de la façon suivante : 0000:7C00c'est à dire segment:offset.

La mise en bouche étant faite, quelle est la suite ?